智能水表项目 - 梅花针旋转角度测量方法

梅花针作为水表的最后一位指针，在水表出厂前，需要检测水表指针的准确性，因此需要对梅花针进行视觉检测。梅花针在外形上具有中心对称的特点，因此传统方法（如关键点匹配等）无法测量其旋转的角度。本文介绍了一种新型梅花针角度测量方法，首先以梅花针的质心为中心进行圆环展开，展开后的梅花针图像近似于信号中的方波。将图像压缩为一维信号，将指针旋转问题转换为信号平移问题，通过求解频域相移求解指针的角度变化。
该方法能在帧率有限的情况下测量梅花针中低速的旋转角度，速度较快，鲁棒性较高，有实际的工程意义。

一、 圆环展开

水表梅花针的外观如图所示。首先使用圆环展开，以梅花针圆心为展开中心，以梅花针半径为展开半径，使用最邻近插值法将梅花针区域进行圆环展开。展开后的图像如图所示，其中图像横轴可以视为角度，纵轴为半径信息。

为了观察图像，将原图灰度化并沿X轴方向进行一定程度的延展。可以观察到，经圆环展开后，图像呈现周期性的方波信号。

二、 信号转换

由于当前图像的信号形式为二维的图像，需要转换成一维的信号。因此可以将图像的Y方向求像素亮度的平均值。由于图像下半部分是梅花针的圆心部分，不具有参考性，因此在求平均，对图像上半部分增加权重。可以得到X轴为角度(0-360), Y轴为像素亮度平均值的信号曲线。
令角度与亮度平均值的函数为f(n)，其频域信号为F(k)。根据离散傅里叶变换，可以得到其频域信号为：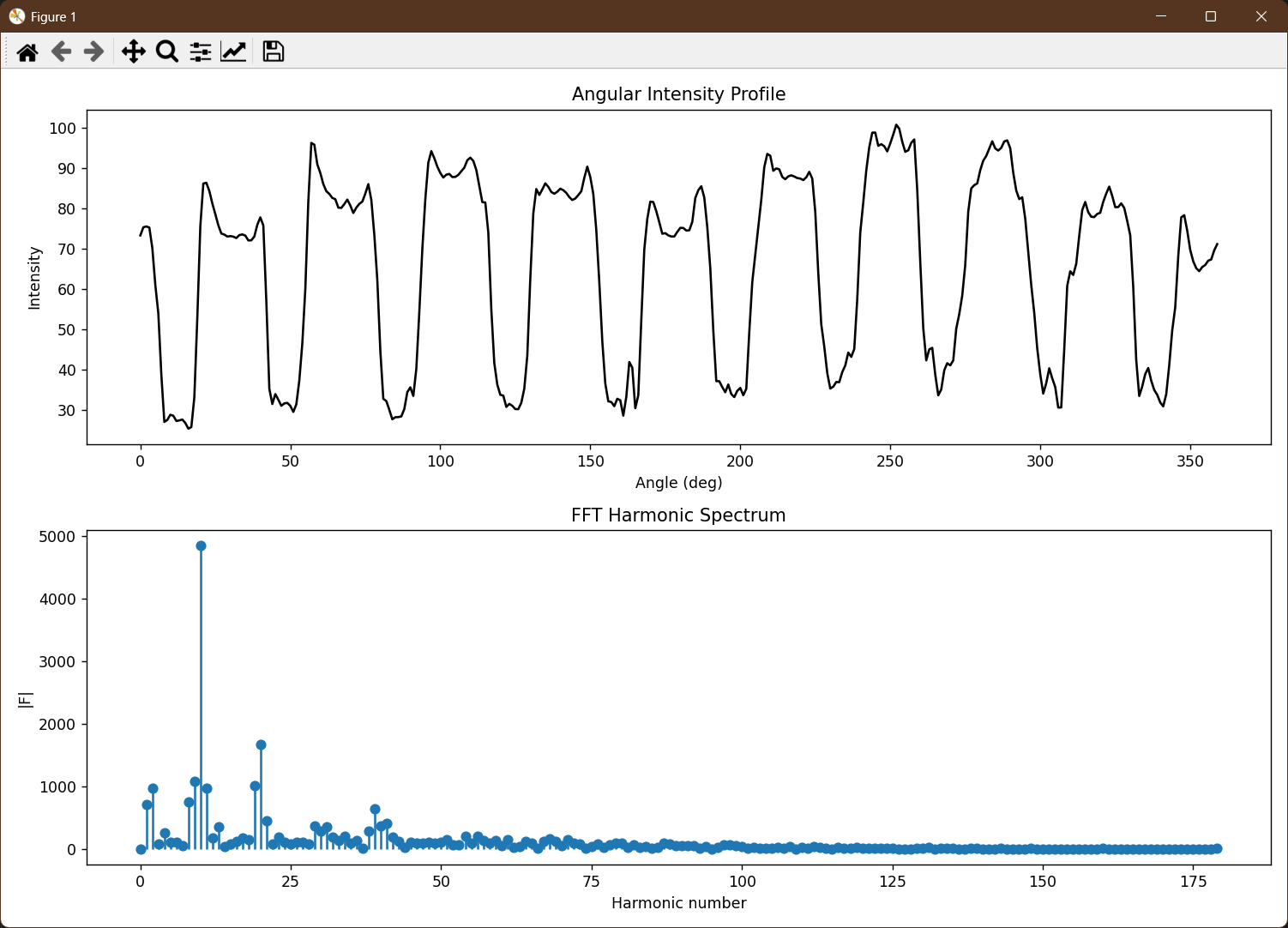

三、 相位转换

当梅花针转动时，其波形f(n)表现为信号的平移，因此可以将计算梅花针的转动角度的问题转换为求解信号f(n)的时移问题。常见的求取时移的方法为求解频域信号的相位变化。在工程应用中常用FFT求解频域信号，FFT为离散傅里叶变换(DFT)的快速算法，其中N点DFT的定义为:

当时域序列发生时移时有性质:

转换到本算法中，时移即为相邻两帧梅花针的旋转的角度。由于梅花针图像展开的信号周期为梅花针齿数，因此可以计算得到相邻两帧的频域相位差为:

反解得到时域时移为：

为减少运算量，提高算法准确性，只取谐波处的相位差进行计算，即k=梅花针齿数。

四、 相位跳变

梅花针转动后，其累计角度等于前一帧图像转换的的信号与得到的角度差的累和。但是由于DFT的相位取值范围是(−π, π]，为了避免在端点处发生跳变，因此相位差的计算需要在复指数域进行：

五、 相位模糊

当梅花针转动速度过快或采集帧率过低时，相邻两帧测得的相位差或时，测量结果与旋转真值相差，即相位模糊问题，据此可以计算出梅花针转动速度的上限。

令梅花针齿数为N，相机采集帧率为FPS，则展开后的波形间隔角度为：

此为可测得的单次转动角度上限。因此可测得的转动速度上限为:

以10齿梅花针，相机采集帧率为60fps为例，其理论识别速度上限为360RPM。但实际上由于旋转的方向问题，角增量的范围是，由于梅花针的旋转方向固定这个先验信息，可以添加一个固定的偏移量使得角增量的范围达到。但是当梅花针静止时，由于增量都为正值，会造成累计误差。因此需要设置一个阈值()屏蔽掉低速的相位抖动以防止静差的累计。

六、实验

采用固定转速的步进电机作为真值，分别测量了10齿梅花针20-240RPM转速的结果以验证算法有效性。由于真值是转速，因此以测量的20秒的平均RPM作为测量值。

测量结果如下：

转速真值/RPM	测量值/RPM	相对误差/%
20	20.020	0.100
40	40.050	0.125
60	60.077	0.128
80	80.100	0.125
100	100.127	0.127
120	120.151	0.125
140	140.175	0.125
160	160.200	0.125
180	180.225	0.125
200	200.250	0.125
220	220.272	0.124
240	240.302	0.126